Energy & Propulsion‎: CrossFire Fusion Reactor¹

Redirecting to the latest CrossFire Fusion Reactor Concept ... 10

CrossFire Fusion Reactor - Core Assembly
Patent Pending PCT/IB2008/054254

The Magnetic and Electrostatic Nuclear Fusion Reactor, or simply CrossFire Fusion Reactor, is a nuclear fusion reactor whose fundamental idea was conceived in 2008 by “Douglas” F. Palte, in order to overcome inherent limits of previous fusion approaches in producing fusion energy at significant rates.
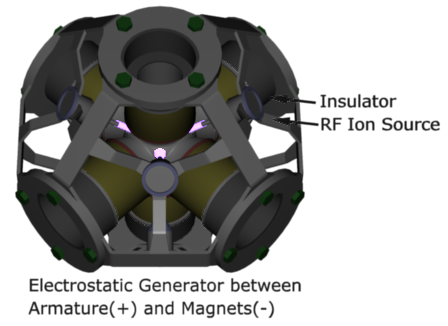
The CrossFire Fusion Reactor uses six superconducting magnets to form a magnetic cusp region where positive ions are injected. At the magnetic cusp region, a negative voltage is applied, and at the opposite end of each magnet, a positive voltage is applied. The ions are accelerated electrostatically towards the negative potential passing through the magnetic cusp reaching the chamber interior, where the ions are confined radially by magnetic fields, and longitudinally by electric fields. The ion injection is done continuously, surrounding the magnetic cusp region to perform a three-dimensional injection. The positive voltage is controlled to confine only reactants, thus allowing the products from the fusion reactions to escape.

Comparison to previous concepts

CrossFire Fusion Reactor - Superconducting Magnet

The CrossFire Fusion Reactor combines features of many other fusion concepts such as Farnsworth–Hirsch Fusor^[1], Bussard Polywell^[2], Limpaecher Plasma Containment^[3], Magnetic Mirror Machines and Penning Trap, but it differs significantly from all of them. It is most closely related to Farnsworth–Hirsch Fusor and Bussard Polywell^[4]^[5], but it diverges from Farnsworth–Hirsch Fusor because it does not have an inner grid. It is also unlike the Bussard Polywell as it does not have recirculation of electrons while it has a well-defined voltage setup and an escape mechanism. The Polywell accelerates and confines positive ions through their attraction to negatively charged electrons, whilst the CrossFire Fusion Reactor does this using a negative voltage applied at the core region.
The initial design was originally based on a stellated polyhedron, accelerating electrostatically reactants inwardly to the central edges and products escaping from the peripheral vertices, after overcoming the electric fields. Magnets were added to act as Penning Trap on the distal ends, and to act as a magnetic mirror at the core region, confining efficiently the plasma while allowing surrounding ion injection, and controlled escaping.

Apparatus and Operation

CrossFire Fusion Reactor - Power Plant

In terms of apparatus, the CrossFire Fusion Reactor consists of a cluster of superconducting magnets, preferably six, pointing to the core region to form magnetic cusps, a set of ion sources surrounding this region, a set of electric insulators on the distal end of each magnet, and an armature to sustain the assembly. A negative voltage is applied at the cusp region and a positive voltage is applied at the armature. Each magnet has a set of independent flat pancake coils grouped together to be adjusted for controlling the level of confinement and escaping.
In terms of operation, the set of ion sources ionizes the fusion fuel exchanging electrons with the electric ground potential producing positive ions. The positive ions fall down toward inwardly the core region, passing through the magnetic cusps, reaching the chamber interior where the ions are confined radially by magnetic fields and trapped longitudinally by electric fields at the end of each magnet. The ions describe a helical orbit around the magnetic field lines, keeping away from the magnet walls. The magnetic cusps act as a magnetic mirror and the continuous ion injection makes the confinement at this region more efficient yet, i.e., the ions do not escape through the cusps due to magnetic mirror effect and continuous ion injection. When a fusion reaction takes place, its charged products overcome the confinement electric field, and can be directed for electricity production and propulsion.

Power Generation

Steam turbines can be optional when using aneutronic fuel^[6]^[7]. A method of energy conversion from positive ions into electricity consists of a positive voltage to produce an electric field to slow down the ions, converting their kinetic energy to potential energy, and an electron gun to neutralize them. The electron gun extracts electrons from a positive terminal of a capacitor which increases its stored energy (E=½CV²). The electron gun current versus the positive voltage is the electric power (P=V×I).^[8]^[9]
Furthermore, the fusion products, after being neutralized, can thrust a spacecraft directly, providing an ISP of over 1 million seconds.^[10]

Advantages

Possibility of using advanced fusion fuels^[11] like hydrogen-boron and Helium-3^[12] producing low neutron hazards.
No inner grid^[13], no recirculation of electrons to cause excessive cusp losses and Bremsstrahlung radiation^[14], more a well-defined voltage setup allowing a great electrostatic acceleration with low energy consumption.
Escape mechanism suitable for electricity generation and propulsion.
Moderate energy consumption, continuous operation, which implies in a possibility of net gain, i.e., chance to have come close to the break-even point at which the device releases as much energy as is required to sustain a fusion reaction.

Requirements

The magnetic fields necessary to confine the plasma should be generated preferably by superconducting magnets, in order to sustain a controlled nuclear fusion reaction.
In case of aneutronic fusion, the magnet bore coating should be composed of alternate layers of tungsten and boron carbide(W/B₄C)^[15]^[16]^[17], in order to reflect Bremsstrahlung radiation, mostly in X-ray range, back to plasma.
The armature must be robust to hold the magnets, because the opposite magnetic fields to bottle the ions are very strong, tending to force the magnets apart.
The fuel should be ionized with a predefined charge-to-mass ratio, and basic calculations must be done for dimensioning magnetic flux and electric voltages.^[18]
The charge-to-mass ratio should be as low as possible, keeping the plasma in a quasi-neutral state, which requires stronger magnetic and electric fields.
The fuel injection must be well-dosed in small quantity, in order to prevent uncontrolled magnetic reconnection that could damage the magnets.^[19]

Basic Calculation

Nuclear fusion energy can be most commonly released from fusion fuels such as hydrogen, deuterium, tritium, helium, lithium, beryllium and boron. The isotopes having potential for third generation fusion fuel are hydrogen-1, helium-3^[20], lithium-6, lithium-7 and boron-11:^[6]^[21]

Reactants

Products

Energy Density

¹H

+ 2

⁶

→

⁴He + ( ³He + ⁶Li) → 3 ⁴He + ¹H

20.9

MeV

153

T J/kg

GWh/kg)

¹H

⁷

→ 2

⁴He

17.2

MeV

204

TJ/kg

GWh/kg)

³He

→

⁴He + 2 ¹H

12.9

MeV

205

TJ/kg

GWh/kg)

¹H

¹¹

→ 3

⁴He

8.7

MeV

TJ/kg

GWh/kg)

The aneutronic reactions showed above are of notable interest due to low emission of neutrons, production of charged particles in the primary reactions, that can be directly convertible into electricity.^[22]^[9]
Examples of boron hydrides are diborane B₂H₆, pentaborane B₅H₉, and decaborane B₁₀H₁₄.
The following example of calculation use pentaborane (B₅H₉):

(¹H + ¹¹B) + 123keV → 3 ⁴He + 8.68MeV

There are 5 × (¹H + ¹¹B) reactions and a rest of 4 × (¹H)

Electronvolt (eV) is a unit of energy and Volt (V) is a unit of electric voltage.
Electronvolt to Joule: 1 eV = 1.60218×10^-19J
Electronvolt to temperature: 1 eV = 11604.505 Kelvin → 1 eV = 11604.505 K -273.15 = 11331.355 °C
Electronvolt to mass: 1 eV = 1.782662×10^-36 kg → 1 MeV = 1.782662×10^-30 kg

particle	charge	mass
proton	+1.60218×10^-19 C	1.67262×10^-27 kg
neutron	0 C	1.67493×10^-27 kg
electron	-1.60218×10^-19 C	0.00091×10^-27 kg

¹¹B mass= 5 protons + 5 electrons + 6 neutrons =

5×1.67262×10^-27 + 5×0.00091×10^-27 + 6×1.67493×10^-27 = 18.41723×10^-27 kg

¹H mass= 1 proton + 1 electron =

1×1.67262×10^-27 + 1×0.00091×10^-27 = 1.67353×10^-27 kg

Pentaborane (B₅H₉) mass: 5×18.41723×10^-27 + 9×1.67353×10^-27 = 107.14792×10^-27 kg

Specific energy of pentaborane (eV/kg):

5 × (8.68MeV-123keV) / (107.14792×10^-27 kg) = 3.99308×10³² eV/kg

Specific energy of pentaborane(J/kg):

3.99308×10³² × 1.60218 ×10^-19 = 63.97633×10¹² J/kg

Specific energy of pentaborane(GWh/kg):

63.97633×10¹² / (3.6×10⁶) = 17.77120×10⁶ kWh/kg = 17.77120 GWh/kg

Extracting 3 electrons from pentaborane to produce positive ions:

107.14792×10^-27 -3×0.00091×10^-27 = 107.14519×10^-27 kg

Charge-to-mass ratio of pentaborane(C/kg) after extracting 3 electrons:

3×1.60218×10^-19 / 107.14519×10^-27 = +4.48600×10⁶ C/kg

The specific energy and charge-to-mass ratio are essential parameters to define the magnetic flux and electric voltages.

Using the specific energy to find the velocity of products from nuclear reaction:

E=½mv² → v= ((E/m) × 2)^0.5 → v= ((63.97633×10¹²) ×2) ^0.5 → v=11.31162×10⁶ m/s

Specific impulse: 11.31162×10⁶ / 9.80665 = 1.15346×10⁶ s

Defining the magnet bore about 0.9 meter (0.45 meter of internal radius) and using the charge-to-mass ratio to find magnetic flux:

r=mv/qB → r= (v/B) × (m/q) → r= (v/B) / (q/m) → B=v/(r × (q/m)) →

B=11.31162×10⁶ / (0.45×4.48600×10⁶) = 5.60341 Teslas

A superconducting magnet of 6 Teslas or higher and about 0.9 meter of bore is sufficient to confine radially the plasma (reactants and products).

Calculation of a negative voltage for electrostatic acceleration of the positive ions to gain enough kinetic energy, at least 123keV, hence 550keV should be enough:

E = q×V → V=E/q → V= (E/m)/ (q/m) →

V= ((5×550keV×1.60218×10^-19)/107.14519×10^-27)/ 4.48600×10⁶ = 916.66667×10³ Volts

Temperature: 550×10³× (11604.505 K -273.15) = 6.23224 billion °C

A negative voltage of -920 kV is enough for the positive ions gain the required kinetic energy, equivalent to 6.2 billions °C.

Calculation of a positive voltage to trap longitudinally the reactants allowing the charged products to escaping. A kinetic energy choice between reactants 550keV and products 8.68MeV could be something about 1.5MeV:

E = q×V → V=E/q → V= (E/m)/ (q/m) →

V= ((5×1.5MeV×1.60218×10^-19)/107.14519×10^-27)/ 4.48600×10⁶ = 2500×10³ Volts

V = 2500×10³ - 920 kV = 1580×10³ Volts

A positive voltage of 1580 kV is enough to trap the reactants allowing the products to escape.

The consumption of a fusion reactor at power of 500MWatts using a fuel with specific energy of 63.97633×10¹²J/kg:

500MW = 500×10⁶ J/s → 500×10⁶ J/s / 63.97633×10¹² J/kg = 7.81539×10^-6 kg/s

A fuel consumption of 7.82 milligrams per second is enough for producing 500MWatts.

Ion source current: 7.81539×10^-6 kg/s × 4.48600×10⁶ C/kg = 35.05989 C/s

The ion source must provide a current of at least 35.1 Amperes for producing 500MWatts.

Cyclotron frequency: f= qB/ (2πm) = (q/m) × (B/2π) = 4.48600×10⁶ × 6/ (2×3.14159) = 4.28382 MHz
Magnetic pressure: pm = B²/2µ° = 6²/ (2×4π×10^-7) = 14.32394×10⁶ J/m³

14.32394×10⁶ / 101325 = 141.36634 atmospheres